(251e) A Combinatorial Bender’s Cuts Approach for Cost Minimization of Network Scheduling Problems with Mixed-Integer and Mixed-Integer Nonlinear Applications

In process industries, scheduling stands out as a relevant decision-making process, typically spanning time horizons ranging from days to months¹. Despite the advances in the field, the efficient solution of many large-scale Mixed-Integer Linear Programming (MILP) and Mixed-Integer Nonlinear Programming (MINLP) scheduling problems still requires the development of reliable algorithms to increase the industrial applicability of scheduling solutions^2,3. A critical factor that makes the solution of large-scale MILP or MINLP network scheduling problems a relevant problem in chemical engineering is the need for integrated decision-making in process industries. Such integration is crucial to avoid suboptimal and infeasible business and plant-level decisions, leading to reduced operating costs and higher revenues¹. For example, integrated scheduling and planning may require the solution of a larger MILP scheduling problem with an extended scheduling horizon that is long enough to incorporate tactical planning decisions, making it difficult to achieve a guaranteed global optimal solution^4,5. Furthermore, the optimization problem becomes an MINLP if scheduling and transient decisions are considered simultaneously⁶; moreover, it may be required to solve this MINLP in very short times (e.g., seconds or minutes) if a rigorous integration technique such as model predictive control is deployed⁷. Advances in optimization strategies to efficiently address MINLP and MILP scheduling problems are thus needed to promote the development of integrated decision-making solutions.

A solution strategy for cost minimization scheduling problems with a discrete-time State Task Network (STN) representation is presented in this work. The proposed method takes advantage of a reformulation of the STN problem⁸, which allows the decoupling of discrete batching-assignment decisions from the remaining variables of the problem. The reformulated version of the problem allows for the application of a new algorithm that implements combinatorial Bender’s cuts, where batching-assignment variables are considered as complicating variables. Conventional Bender’s decomposition strategies would solve the problem by iteratively optimizing a group of complicating variables (e.g., batching and assignment decisions) in a main problem, followed by the solution of the remaining variables in a subproblem with complicating variables fixed⁹. What makes the proposed decomposition strategy different from other methods available is that subproblems do not keep complicating variables fixed; instead, complicating variables are constrained in the subproblems by delimiting the objective function. Consequently, each subproblem is reduced to a feasibility problem, whose solution allows for the removal of multiple infeasible candidates per iteration. This method is expected to speed up the solution of the problem when compared to simple no-good cuts that only exclude one infeasible combination of complicating variables per iteration. Stronger Bender’s cuts can also be derived for this problem; however, these cuts may be invalid, i.e., they may cut off feasible combinations of complicating variables that may improve the objective function¹⁰. On the contrary, the proposed combinatorial Bender’s cuts are valid. In addition, this strategy is designed to handle both MILP and MINLP scheduling problems.

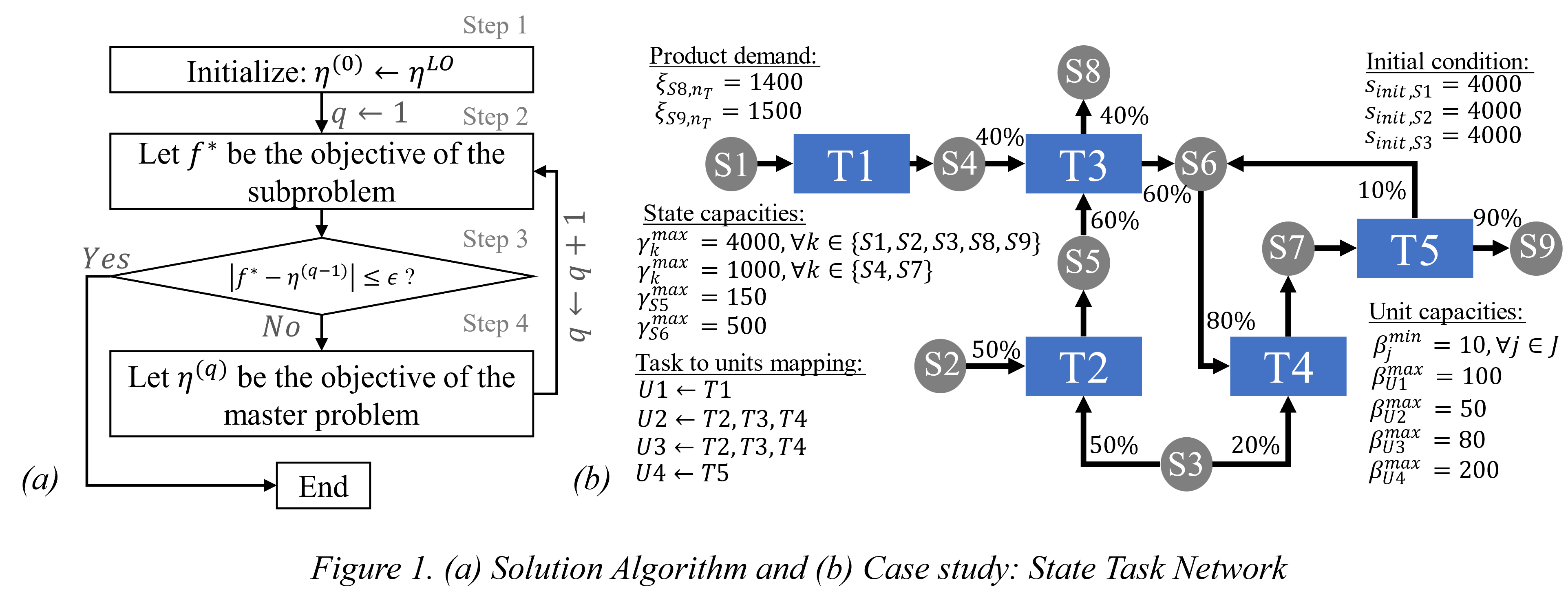
The step of the proposed combinatorial Bender’s cuts approach can be summarized as follows. In the initialization step (i.e., step 1), a lower bound for the objective function is obtained by first solving the relaxed version of the original optimization problem, i.e., Relaxed-MILP (RMILP) or Relaxed-MINLP (RMINLP). The solution to this relaxed problem returns an objective value η^R. Then, this bound is further improved to satisfy the discrete requirement of complicating variables, returning lower bound η^LO. After the initialization step, an iterative procedure starts at step 2, where the feasibility subproblem is solved. This feasibility subproblem is a combination of the original unmodified STN problem plus a constraint that bounds the objective function below by η^LO and returns objective function f^*. After that, the objectives of the main problem (η^LO) and the subproblem (f^*) are compared in step 3 to verify if they lie within the user-defined absolute optimality gap ϵ. If |f^*- η^LO|≤ ϵ, then STOP, as an optimal solution has been found; otherwise, a main problem that incorporates the constraints originally imposed over complicating variables plus a combinatorial Bender’s cut that excludes combinations of complicating variables that are already known to yield infeasible solutions based on previous iterations (step 4). The optimal objective function of this main problem is used to update η^LO; then, a new iteration begins at step 2. Suppose the main problem is solved to optimality. If a reliable strategy is used to find feasible solutions or prove the infeasibility of the subproblem, then the proposed methodology guarantees convergence to a solution with global optimality characteristics. Also, no requirements were enforced over the problem’s constraints; thus, they can be modified to include additional constraints if required, e.g., nonlinear dynamics or nonlinear scheduling relationships. Therefore, the proposed approach can be applied to both MILP and MINLP scheduling problems.

A multiproduct batch plant was used to illustrate the application of this strategy to MILP and MINLP scheduling problems. The MILP version of the problem considers an optimization instance proposed in a previous work⁸. Afterward, the fraction of materials transferred between tasks and states in the STN was allowed to vary to obtain the MINLP instance, adding multiple bilinear terms to the formulation. This type of bilinear term appears in simultaneous scheduling and control problems¹¹. The STN considered in this study is shown in Figure 1. The scheduling horizon considers 120 discretization points, resulting in 2072 continuous variables, 968 binary variables, and 8 integer variables for the MINLP version of the problem. CPLEX and DICOPT were used as both feasibility solvers and benchmarks for the MILP and MINLP cases, respectively, with an optimality gap ϵ=0. Note that other local and global MINLP solvers were also tested, but DICOPT showed the best performance when combined with its feasibility pump¹². The problems were implemented in Pyomo 6.2, and solved using the solvers available through GAMS 34.3.0 in a PC Intel(R) Core(TM) i7-8550U CPU @ 1.80GHz with 16 GB RAM. For the MILP instance, the proposed algorithm was able to reduce the solution time needed by CPLEX, showing a reduction in the time required to close the optimality gap from 1739 seconds to 39 seconds. For the MINLP instance, a time limit of 18000 seconds was imposed. While the proposed algorithm closed its optimality gap after 82.38 seconds, DICOPT reached the time limit and was not able to close its optimality gap below 6.94%. Based on these results, this work brings novelty to the current literature by developing an efficient solution method for large-scale network-based scheduling problems with both MILP and MINLP applications. Perspectives on extending the proposed algorithms to handle other objectives, e.g., profit maximization or makespan minimization, expanding the method to consider other modeling formulations such as continuous time or multiple grid formulations, and extending the applicability to scheduling and control problems that incorporate dynamic process models are also included.

References

1. Shobrys DE, White DC. Planning, scheduling and control systems: why cannot they work together. Computers & Chemical Engineering. 2002;26(2):149-160. doi:10.1016/S0098-1354(01)00737-2
2. Castro PM, Grossmann IE, Zhang Q. Expanding scope and computational challenges in process scheduling. Computers & Chemical Engineering. 2018;114:14-42.
3. Velez S, Maravelias CT. Advances in mixed-integer programming methods for chemical production scheduling. Annu Rev Chem Biomol Eng. 2014;5:97-121.
4. Maravelias CT. Mixed-Time Representation for State-Task Network Models. Ind Eng Chem Res. 2005;44(24):9129-9145. doi:10.1021/ie0500117
5. Menon KG, Fukasawa R, Ricardez-Sandoval LA. Integration of Planning and Scheduling for Large-Scale Multijob Multitasking Batch Plants. Ind Eng Chem Res. 2024;63(2):1039-1054. doi:10.1021/acs.iecr.3c02408
6. Liñán DA, Ricardez-Sandoval LA. Discrete-Time Network Scheduling and Dynamic Optimization of Batch Processes with Variable Processing Times through Discrete-Steepest Descent Optimization. Ind Eng Chem Res. 2024;63(10):4478-4495. doi:10.1021/acs.iecr.3c03455
7. Caspari A, Tsay C, Mhamdi A, Baldea M, Mitsos A. The integration of scheduling and control: Top-down vs. bottom-up. Journal of Process Control. 2020;91:50-62. doi:10.1016/j.jprocont.2020.05.008
8. Velez S, Maravelias CT. Reformulations and Branching Methods for Mixed-Integer Programming Chemical Production Scheduling Models. Ind Eng Chem Res. 2013;52(10):3832-3841. doi:10.1021/ie303421h
9. Hooker JN. Logic-Based Benders Decomposition for Large-Scale Optimization. In: Velásquez-Bermúdez JM, Khakifirooz M, Fathi M, eds. Large Scale Optimization in Supply Chains and Smart Manufacturing: Theory and Applications. Springer Optimization and Its Applications. Springer International Publishing; 2019:1-26.
10. Maravelias CT, Grossmann IE. A hybrid MILP/CP decomposition approach for the continuous time scheduling of multipurpose batch plants. Computers & Chemical Engineering. 2004;28(10):1921-1949.
11. Santander O, Baldea M. Control-aware batch process scheduling. Computers & Chemical Engineering. 2021;152:107360. doi:10.1016/j.compchemeng.2021.107360
12. Bernal DE, Vigerske S, Trespalacios F, Grossmann IE. Improving the performance of DICOPT in convex MINLP problems using a feasibility pump. Optimization Methods and Software. 2020;35(1):171-190. doi:10.1080/10556788.2019.1641498