(84ag) Analysis of Internal Flow Phenomena in a High Speed Rotating Cylinder Using Double Parabolic Axial Flow Model

Author : Dr. Sahadev Pradhan

Affiliation : Chemical Technology Division, Bhabha Atomic Research Centre, Mumbai-400 085, India.

ABSTRACT:

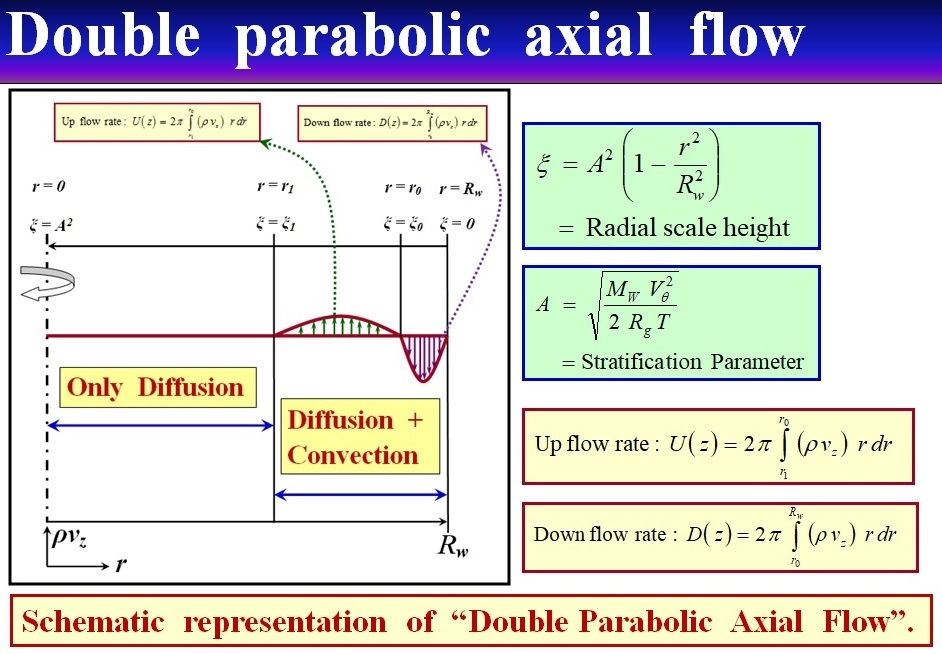
In this study we investigate the internal flow phenomena in a high speed rotating cylinder using double parabolic axial flow model for wall pressure in the range 20 to 100 m-bar [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]. These includes the quantitative estimation of the important process parameters L₀, L, m, and (F/L). Here, L₀ is the internal circulation rate at total reflux, L is the actual internal circulation rate, m = L/ L₀ is the internal circulation parameter, (F/L) is the internal reflux ratio, and F is the external feed flow rate. The radial profile of axial mass flux (ρv_z) is specified as a function of radial scale height (ξ) by two parabola. One parabola represents the flow downward in the region near the rotor wall, and the second one representing the upflow adjacent to the downflow. The feed gas introduced into the rotating cylinder is considered to be associated with the upflowing stream ((Pradhan & Kumaran, J. Fluid Mech., vol. 686, 2011, pp. 109-159); (Kumaran & Pradhan, J. Fluid Mech., vol. 753, 2014, pp. 307-359)). An important finding is that as the wall pressure is increased from 20 to 100 m-bar, there is a increase in L₀, L, and m. However, there are important differences. L₀ initially increases at a faster rate and then saturates at high wall pressure. On the other hand the parameters L and m increases monotonically with the wall pressure. The effect of feed flow rate on the parameters L₀, L, and m is also studied and the analysis indicates that as the feed flow rate is increased, the parameters L₀, L, and m increases, and the effect is significant at high wall pressure. The analysis also shows that as the average gas temperature is increased, the parameters L₀, L, and m increases, and the effect is more pronounced at high wall pressure. However, with the increase of wall pressure, the internal reflux ratio (F/L) decreases, initially at a faster rate and then become constant at high wall pressure, which indicates that there is a strong coupling between the process parameters L₀, L, m, and F/L, and the results also reveal that at high wall pressure (hence at high holdup) the separation process takes place under improved equilibrium condition.

Keywords: High-speed rotating flow, Double parabolic axial flow, Internal flow phenomena, High wall pressure.

References:

[1] PRADHAN, S. & KUMARAN, V. 2011 The generalized Onsager model for the secondary flow in a high-speed rotating cylinder. J. Fluid Mech. 686, 109.

[2] KUMARAN, V & PRADHAN, S. 2014 The generalized Onsager model for a binary gas mixture. J. Fluid Mech. 753, 307.

[3] OLANDER, D. R. 1981 The theory of uranium enrichment by the gas centrifuge. Prog. Nucl.

[4] WOOD, H. G. & SANDERS, G. 1983 Rotating compressible flows with internal sources and sinks. J. Fluid Mech. 127, 299.

[5] WOOD, H. G. & BABARSKY, R. J. 1992 Analysis of a rapidly rotating gas in a pie-shaped cylinder. J. Fluid Mech. 239, 249.

[6] WOOD, H.G. & MORTON, J.B. 1980 Onsager’s pancake approximation for the fluid dynamics of a gas centrifuge. J. Fluid Mech. 101, 1.

[7] BIRD, G. A. 1994 Molecular gas dynamics and the direct simulation of gas flows. Clarendon Press, Oxford.

[8] VINCENTI. 1967 Introduction to Physical Gas Dynamics. Wiley, New York.

[9] BIRD, G. A. 1963 Approach to translational equilibrium in a rigid sphere gas. Physics of fluids 6, 1518.

[10] CERCIGNANI, C. 2000 Rarefied gas dynamics. From basic concepts to actual calculations. Cambridge University Press.

[11] SOUBBARAMAYER. 1979 Centrifugation. In Uranium Enrichment (Ed. S. Villani, Springer) 1,

[12] E. RATZ, One-Stage enrichment with centrifuges, Proceedings of the sixth workshop on gases in strong, Rotation, Tokyo, 621-654 (1985).

[13] E. RATZ, An analytical solution for the separative power of a gas centrifuge, Proceedings of the fifth workshop on gases in strong, Rotation, University of Virginia, Charlottesville (1983).