(579e) Metabolic Modeling of Eicosanoid Class Switch during Arachidonic Acid Metabolism in Mouse Macrophage Cells

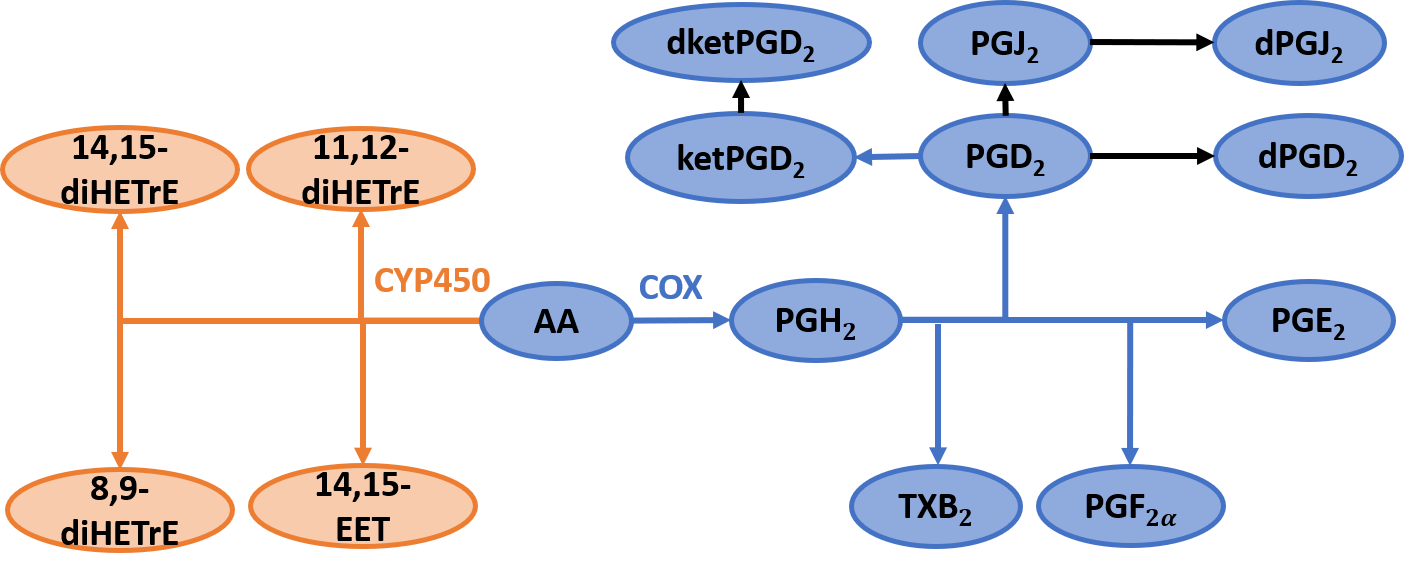
Eicosanoids are a diverse class of bioactive lipids that are derived from polyunsaturated fatty acids, such as arachidonic acid (AA). Eicosanoids play important roles in a wide range of physiological processes, including inflammation and immune function. Eicosanoid class switch is used to describe a process in which the body switches from producing pro-inflammatory to anti-inflammatory eicosanoids. This can occur in response to changes in the availability of different types of polyunsaturated fatty acids, or changes in the activity of the enzymes that convert these fatty acids into eicosanoids. For example, during inflammation, the classic eicosanoid pathway involves the conversion of arachidonic acid to pro-inflammatory eicosanoids such as prostaglandins. Later during the inflammation process, the body switches to producing anti-inflammatory eicosanoids, such as epoxyeicosatrienoic (EET) and lipoxins. Eicosanoid class switching has been implicated in a wide range of physiological processes and pathological conditions, including inflammation and cardiovascular disease. Understanding the mechanisms underlying eicosanoid class switching may lead to the development of new therapeutic strategies for these conditions.

This study aims to mathematically model the eicosanoid class switch in AA metabolism during the inflammatory response. The cybernetic framework, a metabolic modeling technique, is utilized to model the reaction network (shown below). The cyclooxygenase (COX) and cytochromeP450 (CP450) pathways are included in the model. Prostaglandins, formed due to COX activation, are pro-inflammatory; whereas EET and dihydroxyeicosatrienoic (diHETrE), CP450 products, are anti-inflammatory. The cybernetic framework assumes a biological goal. The cybernetic goal is defined and correspondingly the values of cybernetic control variables are computed. The biological goal is proposed as maximizing the pro- and anti-inflammatory responses. The cybernetic goal is formulated as maximizing the sum of the production rates of COX (pro-inflammatory) and CYP450 (anti-inflammatory) products. The cybernetic goal and control variable formulations are shown below. The parameters will be estimated and the model will be simulated to capture the experimental data. The control variables will display eicosanoid class switching, where the pro-inflammatory phase will dominate for a duration, and then the anti-inflammatory response will take over.

Cybernetic goal:

max [ρ_PGH2 +ρ_14,15-EET+ ρ_{14,15-diHETrE} +ρ_8,9-diHETrE + ρ_{11,12-diHETrE}]

Where ρ represents the reaction flux of the metabolite.

Cybernetic control variables:

u_PGH2 =ρ_PGH2 / (⁡ρ_PGH2 +ρ_14,15-EET+ ρ_{14,15-diHETrE} +ρ_8,9-diHETrE + ρ_{11,12-diHETrE} )

u_14,15-EET =ρ_14,15-EET/(⁡ρ_PGH2 +ρ_14,15-EET+ ρ_{14,15-diHETrE} +ρ_8,9-diHETrE + ρ_{11,12-diHETrE})

u_{14,15-diHETrE} =ρ_{14,15-diHETrE}/(⁡ρ_PGH2 +ρ_14,15-EET+ ρ_{14,15-diHETrE} +ρ_8,9-diHETrE + ρ_{11,12-diHETrE})

u_8,9-diHETrE =ρ_8,9-diHETrE/(⁡ρ_PGH2 +ρ_14,15-EET+ ρ_{14,15-diHETrE} +ρ_8,9-diHETrE + ρ_{11,12-diHETrE} )

u_{11,12-diHETrE} =1 - [u_PGH2 + u_14,15-EET+ u_{14,15-diHETrE}+u_{_(8,9-diHETrE)} ]

v_PGH2 =ρ_PGH2/(max⁡[ρ_PGH2 , ρ_14,15-EET , ρ_{14,15-diHETrE} , ρ_8,9-diHETrE , ρ_{11,12-diHETrE} )

v_14,15-EET =ρ_14,15-EET/(max⁡[ρ_PGH2 , ρ_14,15-EET , ρ_{14,15-diHETrE} , ρ_8,9-diHETrE , ρ_{11,12-diHETrE} )

v_{14,15-diHETrE} =ρ_{14,15-diHETrE}/(max⁡[ρ_PGH2 , ρ_14,15-EET , ρ_{14,15-diHETrE} , ρ_8,9-diHETrE , ρ_{11,12-diHETrE} )

v_8,9-diHETrE =ρ_8,9-diHETrE/(max⁡[ρ_PGH2 , ρ_14,15-EET , ρ_{14,15-diHETrE} , ρ_8,9-diHETrE , ρ_{11,12-diHETrE} )

v_{11,12-diHETrE} =ρ_{11,12-diHETrE}/(max⁡[ρ_PGH2 , ρ_14,15-EET , ρ_{14,15-diHETrE} , ρ_8,9-diHETrE , ρ_{11,12-diHETrE} )