2023 AIChE Annual Meeting
(545c) Generative Model Assisted Sampling of Multiscale Dynamical Systems
Authors
Juan Bello-Rivas, Princeton University
Andrew Ferguson, University of Chicago
Ioannis G. Kevrekidis, Princeton University
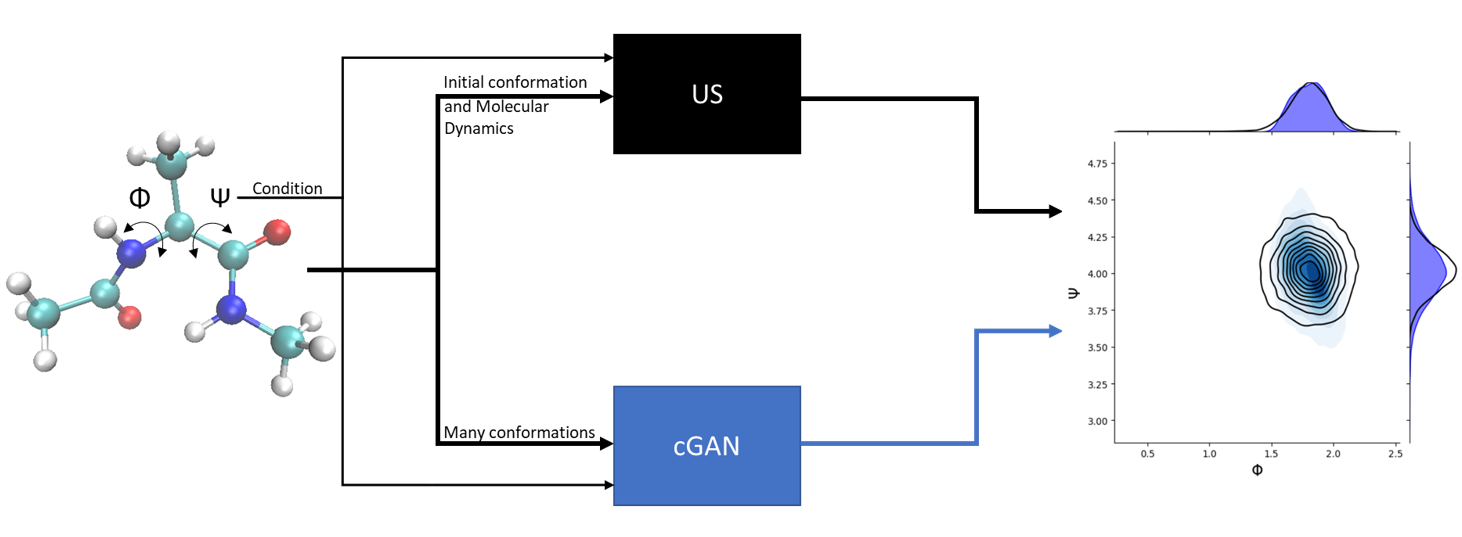
Sampling the phase space of molecular systems -- and, more generally, of complex dynamical systems effectively modeled by stochastic differential equations -- is a crucial modeling step in many applications, from protein folding to materials discovery. These problems are multiscale in nature and can often be described in terms of low-dimensional effective free energy surfaces parametrized by a small number of âslow" reaction coordinates; the remaining âfast" degrees of freedom populate an equilibrium measure on the reaction coordinate values. Over the years, enhanced sampling techniques coupled with molecular simulation have been developed. An intriguing analogy arises with the field of Machine Learning (ML), where generative models such as Score-Based Diffusion Models (SGMs) and Generative Adversarial Networks (GANs) can produce high dimensional samples from probability distributions parameterized by a relatively small number of degrees of freedom. This sample generation returns plausible high dimensional space realizations of a model state, from information about its low-dimensional representation. We present an approach that couples physics-based simulations and biasing methods for sampling conditional distributions with ML-based conditional generative models for the same task. The âcoarse descriptors" on which we condition the fine scale realizations can either be known a priori or learned through nonlinear dimensionality reduction.