(509f) A QR Decomposition Based Parity Space Fault Diagnosis Method for Systems with Numerous Faults

With the increasing complexity of dynamic systems in process industrials, model based fault diagnosis and identification (FDI) problem has attracts more and more wide attention [1], [2]. Considerable research endeavors have recently been devoted to exploring diverse scientific domains, encompassing nonlinear systems [3], stochastic systems [4], and various complex engineering applications [5]. According to [6], observer based approaches and parity space approaches are two main categories of model based methods. Parity space method [7] is characterized by complete decoupling of the initial state influence on the designed residual, which has been studied extensively in many kinds of systems like linear time invariant (LTI) system [8], linear time-varying system[9] and nonlinear systems [10], etc. There are two main techniques for residual generation in the parity space method: directional way and structural way. Multiple research groups have independently demonstrated that the utilization of parity space techniques leads to specific observer structures that exhibit structural equivalence to observer-based approaches, despite distinct design methodologies [11], [12]. Consequently, it is justifiable to incorporate the parity space methodology within the framework of the observer-based fault detection and isolation technique. In fault isolation problems, if the process model and fault model are both known, a new model could be constructed by representing sensor faults and process dynamics faults as pseudo-actuator faults [13], [14]. In this model, the modified state variables are composed of original state variables and measurement variables. As a result, the information of all faults is contained in the modified state. In dynamic systems, if the system is observable, the largest number of faults that could be strongly isolated is the sum of sensor number and the system state variable number, which is proved in observer based techniques [13]. The reason is as follows: if fault number is smaller, the fault incidence matrix is column full rank. Then there is an one-to-one mapping from faults to the state variables and measurements. This statement is also valid in parity space methods because those two categories of methods are structural equivalence. Correspondingly, for parity space and observer based method, if fault number is larger, the residual generator needs to be designed distinguishingly according to different systems. Nevertheless, in chemical processes it is very common that many kinds of faults exist and they could not be strongly isolated. If there is a uniform pattern of residual generators, the generality of the model based FDI approach would be improved in the case of column rank deficient fault incidence matrix. Some immediate and direct techniques to resolve a satisfying parity matrix are required. Unfortunately, the research on contrapuntally solve the design of the residual generator in the case of a large number of faults remains unexplored.

This paper aims to propose a uniform pattern for residual generator designing in the case where fault number is larger, which is very important to complex industrial chemical systems and processes. The approach expands the application of parity space based method to a situation with more constraints.

In this paper, QR decomposition is introduced to parity space approach to obtain an upper triangular structure generator. With the triangular structure, the -th entry in the residual vector is only influenced by the -th entry to the end of fault vector. It could be concluded that if the first to -th residual entry is abnormal, occurring fault(s) must be included in faults which are linked to the first to -th fault entry.

The whole technique could be divided into two steps: firstly, we apply row operation on the fault vector and column operation on the initial fault incidence matrix; secondly, QR decomposition is done on the new incidence matrix. The new residual is monitored and above procedures are repeated under different row and column operations.

By exhaustion on the row operation, the number of abnormal residual entries would reach minimum. Then all occurring faults are traced immediately. The isolation rule is as follows: if the residual vector has the characteristic that there are anomalies in the first to -th entries and the other entries are all normal, it could be verified that the first to -th faults occur in the new fault vector which is obtained by row operation. Finally, fault detection and isolation could be realized simultaneously no matter which faults occur.

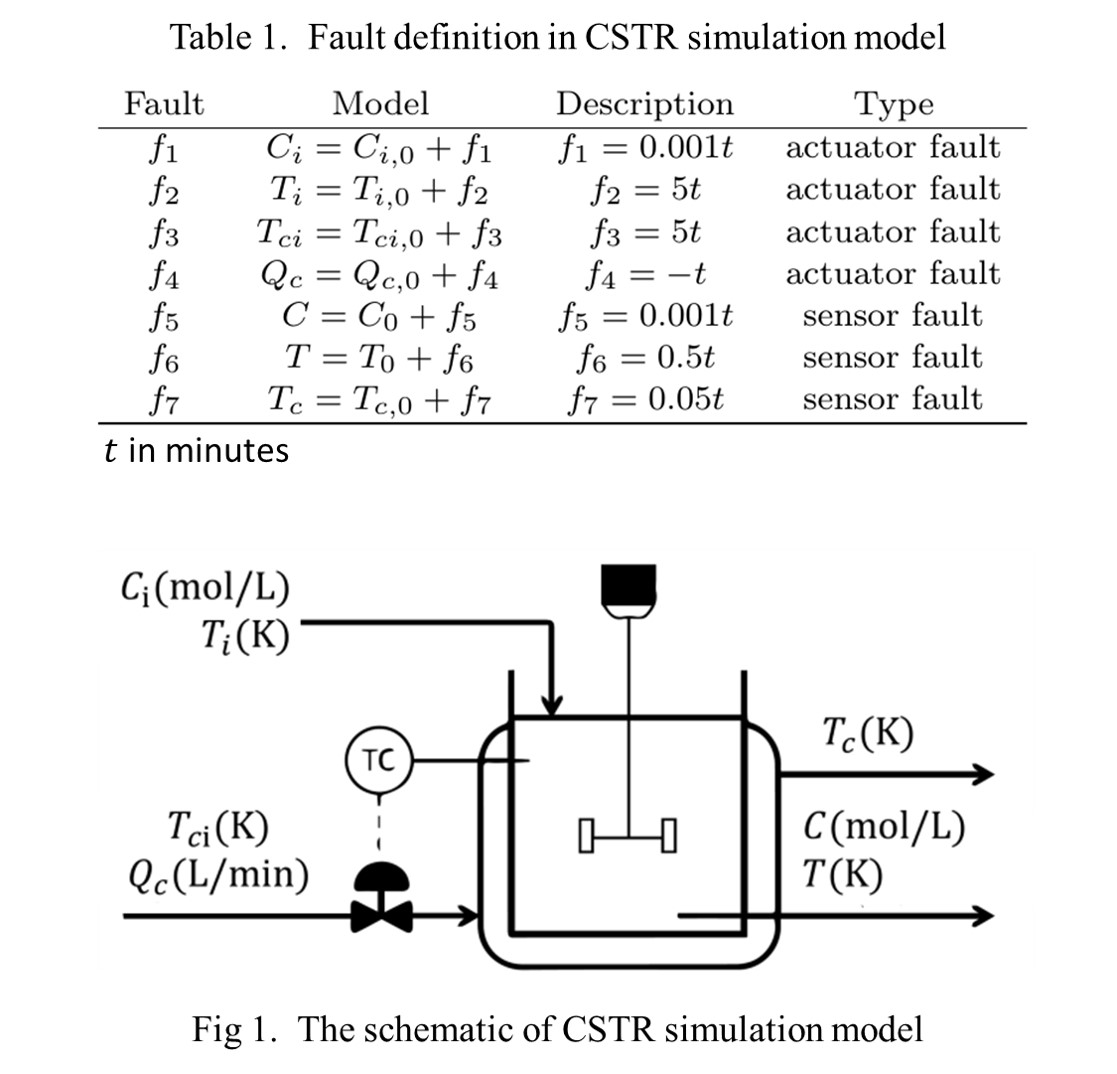
This technique is applied to the fault isolation on an exothermic first order reaction in a simulation Continuous Stirred Tank Reactor (CSTR), a typical system in FDI research [15]. The schematic of CSTR is represented in Fig.1. In this system, C_i and C are inlet and outlet concentration of reactant, T_i and T are temperature of inlet and outlet, T_ci and T_c are temperature of inlet and outlet coolant, and Q_c is the coolant water flow rate. C, T and T_c are thought as state variables. Those variables are also considered as measurement variables in the state space process model. The dynamic behavior are obtained from the first principle. The fault definition is introduced in Table.1. The nonlinear process model parameters in [15] are adopted. Faulty and fault-free datasets are simulated for 20 . In this paper, the nonlinear model is firstly linearized referring to [16].

The contribution of proposed approach is as follows:

1. a direct and immediate approach to design the residual generator and obtain the parity matrix is proposed, together with enlightening examples as tutorials for their practical usages;
2. this study presents a new approach that overcomes the limitations of the traditional parity space method in terms of the number of faults considered in the process. Specifically, the proposed method provides fault isolation conditions that are more easily satisfied for LTI systems.

Overall, this abstract proposes a targeted solution for fault isolation in the situation where the influences of faults on state are independent but the faults in the chemical processes could occur independently. The application details of this work were given via a simulation CSTR example. This work fills in the gaps of applied scenario for parity space method. By introducing QR decomposition, this work offers a universal pattern for designing a residual generator, and makes it easier to find a satisfying parity matrix.

[1] J. Chen and R. J. Patton, Robust Model-Based Fault Diagnosis for Dynamic Systems, vol. 3. Springer US, 1999. Accessed: Nov. 07, 2022. [Online]. Available: http://link.springer.com/10.1007/978-1-4615-5149-2

[2] R. Isermann, ‘Model-based fault-detection and diagnosis – status and applications’, Annu. Rev. Control, vol. 29, no. 1, pp. 71–85, Jan. 2005, doi: 10.1016/J.ARCONTROL.2004.12.002.

[3] S. Dong, Z.-G. Wu, P. Shi, H. R. Karimi, and H. Su, ‘Networked Fault Detection for Markov Jump Nonlinear Systems’, IEEE Trans. Fuzzy Syst., vol. 26, no. 6, pp. 3368–3378, Dec. 2018, doi: 10.1109/TFUZZ.2018.2826467.

[4] Z. Mao, Y. Zhan, G. Tao, B. Jiang, and X.-G. Yan, ‘Sensor Fault Detection for Rail Vehicle Suspension Systems with Disturbances and Stochastic Noises’, IEEE Trans. Veh. Technol., vol. 66, no. 6, pp. 4691–4705, 2017, doi: 10.1109/TVT.2016.2628054.

[5] H. Cheng, J. Wu, Y. Liu, and D. Huang, ‘A novel fault identification and root-causality analysis of incipient faults with applications to wastewater treatment processes’, Chemom. Intell. Lab. Syst., vol. 188, pp. 24–36, May 2019, doi: 10.1016/j.chemolab.2019.03.004.

[6] S. X. Ding, Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms and Tools. London: Springer London, 2013. doi: 10.1007/978-1-4471-4799-2.

[7] J. J. Gertler and R. Monajemy, ‘Generating directional residuals with dynamic parity relations’, Automatica, vol. 31, no. 4, pp. 627–635, Apr. 1995, doi: 10.1016/0005-1098(95)98494-Q.

[8] J. Gertler, Fault Detection and Diagnosis in Engineering Systems. Boca Raton: CRC Press, 2019. doi: 10.1201/9780203756126.

[9] M. Zhong, Y. Song, and S. X. Ding, ‘Parity space-based fault detection for linear discrete time-varying systems with unknown input’, Automatica, vol. 59, pp. 120–126, Sep. 2015, doi: 10.1016/j.automatica.2015.06.013.

[10] J. Gertler and M. Staroswiecki, ‘STRUCTURED FAULT DIAGNOSIS IN MILDLY NONLINEAR SYSTEMS: PARITY SPACE AND INPUT-OUTPUT FORMULATIONS’, IFAC Proc. Vol., vol. 35, no. 1, pp. 341–346, Jan. 2002, doi: 10.3182/20020721-6-ES-1901.00788.

[11] J. J. Gertler, ‘Survey of model-based failure detection and isolation in complex plants’, IEEE Control Syst. Mag., vol. 8, no. 6, pp. 3–11, Dec. 1988, doi: 10.1109/37.9163.

[12] P. M. Frank, ‘Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy: A survey and some new results’, Automatica, vol. 26, no. 3, pp. 459–474, May 1990, doi: 10.1016/0005-1098(90)90018-D.

[13] M.-A. Massoumnia, ‘A GEOMETRIC APPROACH TO FAILURE DETECTION AND IDENTIFICATION IN LINEAR SYSTEMS’.

[14] M.-A. Massoumnia, G. C. Verghese, and A. S. Willsky, ‘Failure detection and identification’, IEEE Trans. Autom. Control, vol. 34, no. 3, pp. 316–321, Mar. 1989, doi: 10.1109/9.16422.

[15] K. E. S. Pilario and Y. Cao, ‘Canonical variate dissimilarity analysis for process incipient fault detection’, IEEE Trans. Ind. Inform., vol. 14, no. 12, pp. 5308–5315, Dec. 2018, doi: 10.1109/TII.2018.2810822.

[16] D. Eriksson, E. Frisk, and M. Krysander, ‘A method for quantitative fault diagnosability analysis of stochastic linear descriptor models’, Automatica, vol. 49, no. 6, pp. 1591–1600, Jun. 2013, doi: 10.1016/J.AUTOMATICA.2013.02.045.