(701b) Risk Mitigation in Model-Based Experiment Design: A Continuous-Effort Approach to Optimal Campaigns

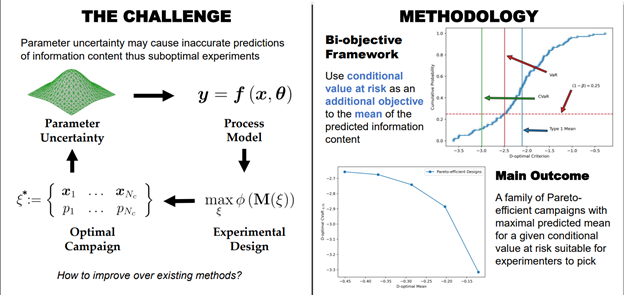
A key challenge in maximizing the effectiveness of model-based design of experiments^1–3 for calibrating nonlinear process models is the inaccurate prediction of information that is afforded by each new experiment⁴. This talk presents a novel methodology to exploit prior probability distributions of model parameter estimates in a bi-objective optimization formulation, where a conditional-value-at-risk⁵ criterion is considered alongside an average information criterion. We describe a tractable numerical approach that discretizes the experimental design space and leverages the concept of continuous-effort experimental designs^6,7 in a convex optimization formulation. We demonstrate effectiveness and tractability through three case studies, including the design of dynamic experiments. In one case, the Pareto frontier comprises experimental campaigns that significantly increase the information content in the worst-case scenarios. In another case, the same campaign is proven to be optimal irrespective of the risk attitude. Through this talk, we also introduce a Python implementation PyDEX (https://github.com/KennedyPutraKusumo/pydex) that handles both nominal, risk-averse, and risk-neutral formulations. PyDEX interfaces with convex optimization solvers through cvxpy⁸ and can either incorporate user-supplied sensitivities or generate them using numerical differentiation⁹.

Available at

Main site : https://github.com/KennedyPutraKusumo/pydex

Stable fork : https://github.com/omega-icl/pydex

References

1. Franceschini, G. & Macchietto, S. Model-based design of experiments for parameter precision: State of the art. Chem. Eng. Sci. 63, 4846–4872 (2008).
2. Atkinson, A. C., Donev, A. N. & Tobias, R. Optimum experimental designs, with SAS. (Oxford University Press, 2007).
3. Fedorov, V. V. & Leonov, S. L. Optimal Design for Nonlinear Response Models. (CRC Press, 2013, 2014).
4. Asprey, S. P., Macchietto, S. & Pantelides, C. C. Robust Optimal Designs for Dynamic Experiments. IFAC Proc. Vol. 33, 845–850 (2000).
5. Rockafellar, R. T. & Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2, 21–41 (2000).
6. Kusumo, K. P., Kuriyan, K., García-Muñoz, S., Shah, N. & Chachuat, B. Continuous-Effort Approach to Model-Based Experimental Designs. in 31st European Symposium on Computer Aided Process Engineering (eds. Türkay, M. & Gani, R.) 50, 867–873 (Elsevier, 2021).
7. Vanaret, C. et al. Two-phase approaches to optimal model-based design of experiments: how many experiments and which ones? Comput. Chem. Eng. 146, 107218 (2021).
8. Diamond, S. & Boyd, S. {CVXPY}: {A} {P}ython-embedded modeling language for convex optimization. J. Mach. Learn. Res. 17, 1–5 (2016).
9. Brodtkorb, P. A. & D’Errico, J. numdifftools 0.9.11. (2015).