Breadcrumb
- Home
- Publications
- Proceedings
- 2022 Annual Meeting
- Computing and Systems Technology Division
- Operation of Energy Systems
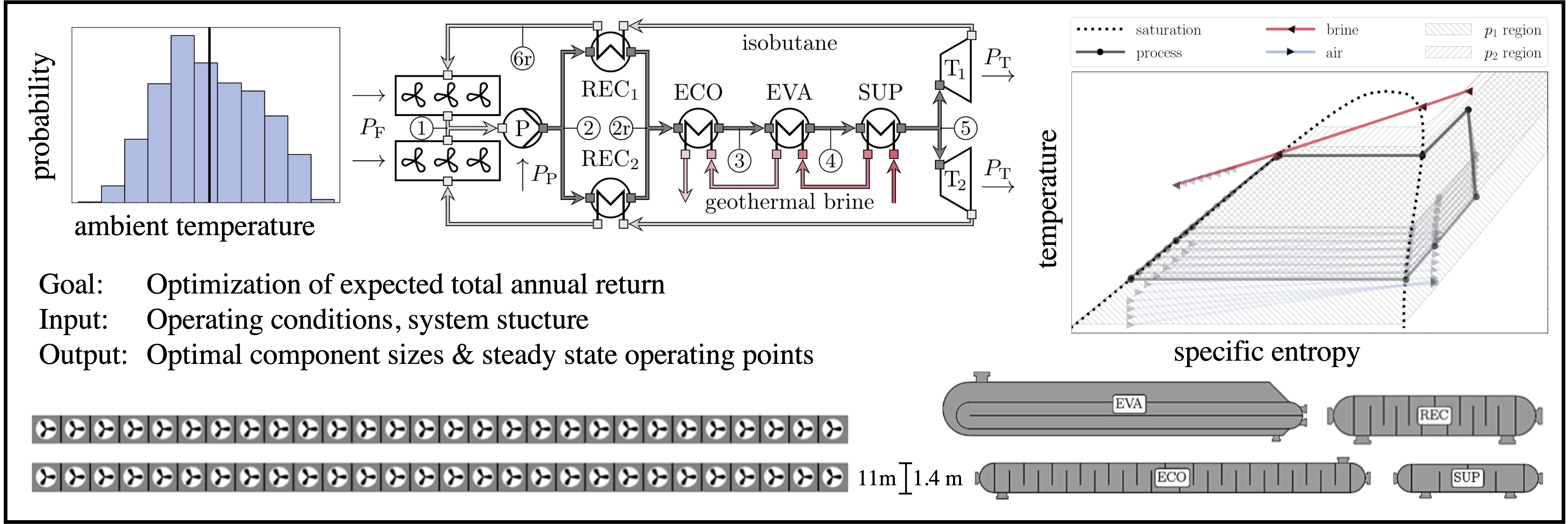
- (690c) Globally Optimal Design and Operation of an Air-Cooled Geothermal Organic Rankine Cycle
2022 Annual Meeting
(690c) Globally Optimal Design and Operation of an Air-Cooled Geothermal Organic Rankine Cycle
Electricity generation from geothermal sources is projected to reach 150 GW of installed capacity by 2050, meeting up to 3% of world electricity demand [1]. For low- and intermediate-temperature reservoirs, organic Rankine cycle (ORC) technology is especially relevant as it is economically preferable to dry or flash steam cycle technology [2]. However, many potential locations for ORCs lack access to cooling water for heat rejection, and thus require the use of air-cooling [3]. Due to the low heat capacity of air, large air-flow rates and thus condenser sizes are required, rendering the air cooling condenser a parasitic energy loss and a major contributor to overall system costs.
To ensure an optimal economic design as well as a wide range of operability, it is crucial to take into account the variable operating conditions implied by different ambient temperatures during system design. A common approach for system design and operation is to first optimize the system for a single operating point, e.g., [4, 5], and subsequently use the resulting design to perform an off-design analysis, e.g., [6, 7, 8], ensuring acceptable operation at other operating points. The downside of such sequential approaches is that the off-design behavior of the system is kept hidden from the optimizer, potentially resulting in suboptimal or even infeasible systems.
Instead, we propose a simultaneous consideration of design and operation within a single optimization problem, as already demonstrated in our previous work on energy system design [9]. Here we apply this approach to a design model for an air-cooled geothermal ORC that incorporates accurate thermodynamic properties of the working fluid via artificial neural networks, empirical heat transfer correlations for all heat exchangers, efficiency- and flow-characteristics, specific to ORC turbines, and costing models for all components [10]. Using this model, we formulate a nonconvex two-stage stochastic programming problem [11, 12], maximizing total annualized revenue (TAR).
We show that a system design optimized for the average or maximum ambient temperature only, is infeasible for parts of the considered siteâs temperature range. In contrast, an optimization considering 11 ambient temperatures along with their relative likelihoods results in a design that is feasible for the entire temperature range. Global optimization for this multiple-temperature problem is computationally challenging, and results in a large optimality gap. Drawing on ideas from stochastic programming [13], we solve multiple smaller subproblems, considering only a single operating point to obtain a valid upper bound on the TAR. This allows for a significant reduction of the optimality gap. The proposed modeling and optimization approach is not only applicable to geothermal ORCs, but also appears promising for other applications, e.g., ORCs for waste heat recovery from industrial processes [14].
To ensure an optimal economic design as well as a wide range of operability, it is crucial to take into account the variable operating conditions implied by different ambient temperatures during system design. A common approach for system design and operation is to first optimize the system for a single operating point, e.g., [4, 5], and subsequently use the resulting design to perform an off-design analysis, e.g., [6, 7, 8], ensuring acceptable operation at other operating points. The downside of such sequential approaches is that the off-design behavior of the system is kept hidden from the optimizer, potentially resulting in suboptimal or even infeasible systems.
Instead, we propose a simultaneous consideration of design and operation within a single optimization problem, as already demonstrated in our previous work on energy system design [9]. Here we apply this approach to a design model for an air-cooled geothermal ORC that incorporates accurate thermodynamic properties of the working fluid via artificial neural networks, empirical heat transfer correlations for all heat exchangers, efficiency- and flow-characteristics, specific to ORC turbines, and costing models for all components [10]. Using this model, we formulate a nonconvex two-stage stochastic programming problem [11, 12], maximizing total annualized revenue (TAR).
We show that a system design optimized for the average or maximum ambient temperature only, is infeasible for parts of the considered siteâs temperature range. In contrast, an optimization considering 11 ambient temperatures along with their relative likelihoods results in a design that is feasible for the entire temperature range. Global optimization for this multiple-temperature problem is computationally challenging, and results in a large optimality gap. Drawing on ideas from stochastic programming [13], we solve multiple smaller subproblems, considering only a single operating point to obtain a valid upper bound on the TAR. This allows for a significant reduction of the optimality gap. The proposed modeling and optimization approach is not only applicable to geothermal ORCs, but also appears promising for other applications, e.g., ORCs for waste heat recovery from industrial processes [14].
References:
[1] O. Edenhofer, R. Pichs-Madruga, Y. Sokona, et al. IPCC special report on renewable energy sources and climate change mitigation. Tech. rep. Working Group III of the IPCC, Cambridge University Press, Cambridge, UK, 2011.
[2] H. Nazif. âFeasibility of Developing Binary Power Plants in the Existing Geothermal Production Areas in Indonesiaâ. In: United Nations University Geothermal Training Programme, Reykjavik, Iceland (2011), pp. 709â735.
[3] E. Macchi and M. Astolfi. Organic Rankine Cycle (ORC) Power Systems: Technologies and Applications. Elsevier, 2017. doi: 10.1016/c2014-0-04239-6.
[4] M. Astolfi, M. C. Romano, P. Bombarda, et al. âBinary ORC (organic Rankine cycles) power plants for the exploitation of mediumâlow temperature geothermal sources â Part A: Thermodynamic optimizationâ. In: Energy 66 (Mar. 2014), pp. 423â434. doi: 10.1016/j.energy.2013.11.056.
[5] M. Astolfi, M. C. Romano, P. Bombarda, et al. âBinary ORC (organic Rankine cycles) power plants for the exploitation of mediumâlow temperature geothermal sources â Part B: Techno-economic optimizationâ. In: Energy 66 (Mar. 2014), pp. 435â446. doi: 10.1016/j.energy.2013.11.057.
[6] G. Manente, A. Toffolo, A. Lazzaretto, et al. âAn Organic Rankine Cycle Off-design Model for the Search of the Optimal Control Strategyâ. In: Energy 58 (Sept. 2013), pp. 97â106. doi: 10.1016/j.energy.2012.12.035.
[7] F. Calise, C. Capuozzo, A. Carotenuto, et al. âThermoeconomic Analysis and Off-design Performance of an Organic Rankine Cycle Powered by Medium-temperature Heat Sourcesâ. In: Solar Energy 103 (May 2014), pp. 595â609. doi: 10.1016/j.solener.2013.09.031.
[8] Y. Nusiaputra, H.-J. Wiemer, and D. Kuhn. âThermal-economic Modularization of Small, Organic Rankine Cycle Power Plants for Mid-enthalpy Geothermal Fieldsâ. In: Energies 7.7 (July 2014), pp. 4221â4240. doi: 10.3390/en7074221.
[9] M. Yunt, B. Chachuat, A. Mitsos, et al. âDesigning man-portable power generation systems for varying power demandâ. In: AIChE J. 54.5 (2008), pp. 1254â1269. doi:10.1002/aic.11442.
[10] M. Langiu, M. Dahmen, and A. Mitsos. âSimultaneous optimization of design and operation of an air-cooled geothermal ORC under consideration of multiple operating pointsâ. In: Comput. Chem. Eng. 161 (May 2022), p. 107745. doi: 10.1016/j.compchemeng.2022.107745.
[11] J. R. Birge and F. Louveaux. Introduction to Stochastic Programming. Springer Science & Business Media, 2011.
[12] P. Kall and S. W. Wallace. Stochastic Programming. John Wiley and Sons Ltd, 1994. isbn: 9780471951087.
[13] A. Madansky. âInequalities for Stochastic Linear Programming Problemsâ. In: Management Science 6.2 (Jan. 1960), pp. 197â204. doi:10.1287/mnsc.6.2.197.
[14] R. Pili, H. Spliethoff, and C. Wieland. âEffect of Cold Source Conditions on the Design and Control of Organic Rankine Cycles for Waste Heat Recovery from Industrial Processesâ. In: 32nd ECOS. 2019