(426g) Maximum Entropy Inference in Chemical Reaction Networks with Unknown Kinetic Parameters

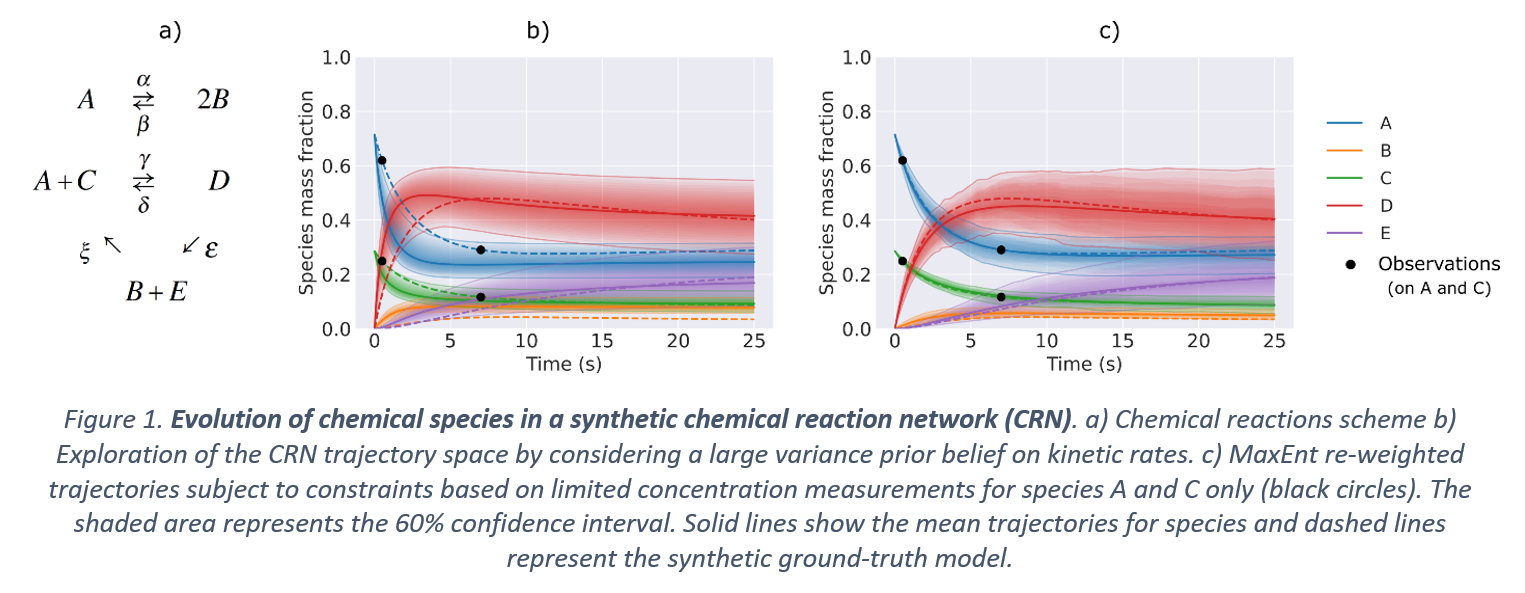
A fundamental problem in the analysis of chemical reaction networks lies in describing the dynamics of species' concentrations with coherency towards available experimental data. This becomes crucial in cases with missing data or when the concentration of certain species cannot be measured due to technical difficulties. A general purpose of the mathematical models describing the reaction networks is to predict the true species' concentrations as a function of time. This is accomplished by using kinetic parameters inferred by various parameter inference methods based on a set of experimental observations. However, these methods mostly rely on high resolution and clean time-series concentration data, which is not typically applicable in experimental settings. We formulate this problem as a simulation-based inference, over a large, but limited, mass-action constrained reaction space and utilize the statistical principle of maximum entropy (MaxEnt) to produce robust, interpretable (bio)chemical reaction networks, as well as uncertainty estimates for the predictions. In specific, we use MaxEnt to infer the concentration dynamics in different systems of chemical reaction networks under the regime of sparse concentration measurements, given a high-variance prior belief on the kinetic rates. To account for the epistemic uncertainty that comes with noisy concentration data obtained by measurement devices, we allow for a bias in agreement in the MaxEnt formulation via a Laplace distribution prior. Moreover, by averaging over multiple measurements within short intervals, we incorporate the aleatoric uncertainty in the system. Our approach is compatible with time-series batch reactor data and for continuous reactor experiments with steady-state concentration measurements.