2022 Annual Meeting
(236f) Pyomo.Doe: An Open-Source Package for Model-Based Design of Experiments in Python
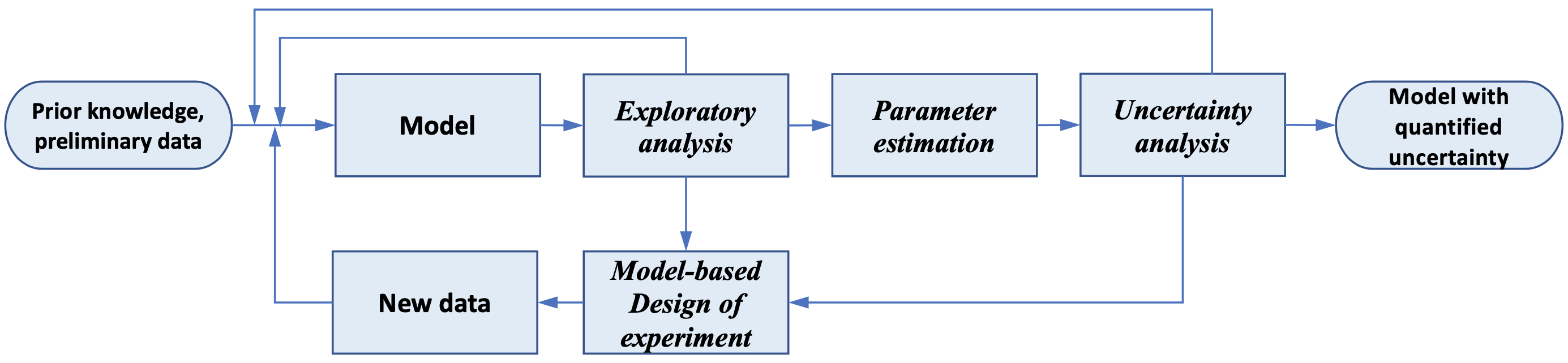
In this work, we present Pyomo.DOE, a general Python package for MBDoE using Pyomo models to help reduce this barrier. Pyomo.DOE accepts Pyomo models representing the experiments, checking the identifiability of the model and suggesting new experiments to provide data for parameter estimation, which can also be accomplished in the Pyomo ecosystem by Parmest [6] as in Fig.1. Pyomo.DOE automatically formulates the MBDoE analysis problems for users and leverages several important numerical enhancements. First, Pyomo.DOE uses a nonlinear sensitivity analysis code k_aug [5] to quickly estimate the Fisher Information Matrix (FIM), reducing the computational cost of assembling the FIM by up to 95% for large-scale problems. Second, Pyomo.DOE uses a new two-stage stochastic programming formulation to automatically formulate and initialize FIM-based MBDoE dynamic optimization problems. Cholesky factorization and scaling are integrated into the problem formulation to improve the numerical robustness of state-of-the-art nonlinear programming solvers such as Ipopt. We also explore nonlinear programming algorithms which iteratively converge the model and use k_aug to quickly compute the FIM. We benchmark this alterative approach against optimization with Ipopt using the stochastic programming formalation.
Two chemical engineering case studies are considered to demonstrate Pyomo.DOE. The first, a reaction kinetics illustrative example, demonstrates the analysis workflow with Pyomo.DOE. We show how Pyomo.DOE identifies and eliminates the unidentifiability of models with highly-correlated parameters. It also shows that two experiments designed by MBDoE can provide the equivalent information as more than ten experiments by random design. In the second study, we consider, for the first time, MBDoE applied to fixed-bed breakthrough experiments to characterize an advanced sorbent for CO2 capture and utilization. The partial differential-algebraic equation (PDE) model couples mass and momentum transport phenomena with adsorption equilibria (isotherms) and kinetics; discretization in space (method of lines) and time (backward finite difference or collocation) results in 23,360 sparse algebraic constraints, and forming the MBDoE problem of 93,861 variables and 93,859 constraints. Pyomo.DOE reveals that the two unknown parameters in the science-based PDAE model cannot be reliably estimated by only measuring the CO2 outlet flowrate. Instead, Pyomo.DOE shows that the collection of additional data, such as measuring the temperature in the fixed-bed column, can improve the information content of experiments by four orders of magnitude. It reveals that MBDoE gives chemical engineers a principled approach to estimate the value of additional measurements or modifications before changing experimental campaigns in the laboratory.
Reference
[1]Franceschini, G., & Macchietto, S. (2008). Model-based design of experiments for parameter precision: State of the art. Chemical Engineering Science, 63(19), 4846-4872.
[2]Waldron, C., Pankajakshan, A., Quaglio, M., Cao, E., Galvanin, F. and Gavriilidis, A., 2020. Model-based design of transient flow experiments for the identification of kinetic parameters. Reaction Chemistry & Engineering, 5(1), pp.112-123.
[3]Balsa-Canto, E., Rodriguez-Fernandez, M. and Banga, J.R., 2007. Optimal design of dynamic experiments for improved estimation of kinetic parameters of thermal degradation. Journal of Food Engineering, 82(2), pp.178-188.
[4]Chakrabarty, A., Buzzard, G.T. and Rundell, A.E., 2013. Model-based design of experiments for cellular processes. Wiley Interdisciplinary Reviews: Systems Biology and Medicine, 5(2), pp.181-203.
[5]Thierry, D. (2019). Nonlinear Optimization-based frameworks for Model Predictive Control, State-Estimation, Sensitivity Analysis, and Ill-posed Problems (Doctoral dissertation, Carnegie Mellon University).
Fig.1: The exploratory analysis, parameter estimation, uncertainty analysis, and MBDoE are combined in an iterating framework to select and validate science-based mathematical models.