(261d) Abradable Particles in DEM through Spherical Harmonics

Abrasion is a particular form of particle attrition in which a particle changes in shape by becoming smoother over time through the preferential removal of protrusions on the particle’s surface. Fines are produced by abrasion which are much smaller than the particle’s size. Abrasion plays a significant role in industrial applications, as does attrition more broadly. Fines can reduce flowability which can impair processing operations such as conveying, blending or tableting [1]. Attrition affects the bulk density, specific surface area, segregation behaviour and dissolution rate which has major implications for the quality of pharmaceutical products [2, 3]. The rehydration characteristics of infant formula are significantly affected by attrition [4]. Abrasion of fluid cracking catalysts is a significant cost factor in these processes as it necessitates the periodic replacement of the catalysts [5].
Because of its importance to a wide range of industrial particulate processes, quantifying abrasion, and ultimately understanding abrasion in order to better control it, are of fundamental importance. DEM simulations have contributed greatly to our understanding of granular materials behaviour in recent years [6], as they give access to particle-scale information such as interparticle contact forces which are difficult, if not impossible, to acquire directly from experiments. Unfortunately, most DEM simulations are based on spherical particles, while our everyday life experience shows that abrasion depends heavily on the particle shape: angular particles are more susceptible to surface breakage than rounded ones. Additionally, simulations of abrasion in DEM are very few and are mostly application-based [7].
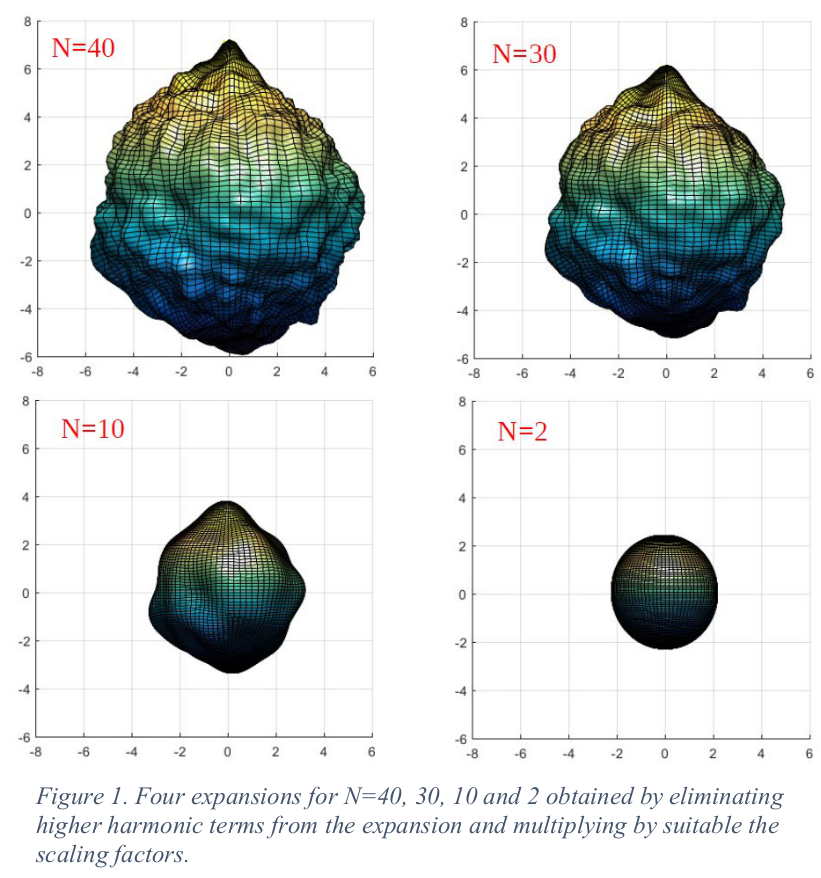
In view of these considerations, a novel approach is presented for modelling non-spherical, abradable particles in DEM. The particle’s shape is described by an expansion in spherical harmonic functions [8], with the high-degree terms mainly responsible for microscopic details of the shape, e.g., the surface texture. Mathematical considerations [9], together with recent experimental results [10], show that higher harmonics, corresponding to the surface texture, are the first to be eroded, while ellipsoidal shapes, found in abundance in nature, take much longer to become spherical, i.e., the sphere is the equilibrium shape [9]. Therefore the abrasion process can be represented through the sequential removal of the highest spherical harmonics (see Fig. 1). During abrasion, mass is lost in the form of fines, and an additional set of scaling factors ensures that the high-degree spherical harmonic expansion, representing the original shape, bounds the expansion at any lower degree: the abraded shape. The sequence of spherical harmonic expansions with decreasing order allows prediction of a particle’s shape evolution during the abrasion process. Finally, this abrasion is related to microscopic wearing laws, based on energy considerations. A comparison between the abraded shapes obtained through the microscopic wearing laws and the predicted shapes is discussed. The implementation of this novel method in the open-source LAMMPS code is presented along with possible sources of performance improvement.

[1] A. Lekhal, K. P. Girard, M. A. Brown, S. Kiang, B. J. Glasser, J. G. Khinast (2003), Impact of agitated drying on crystal morphology: KCl-water system, Powder Technol. 132(2-3): 119–130.
[2] C. Hare, M. Ghadiri, R. Dennehy (2011), Prediction of attrition in agitated particle beds, Chem. Eng. Sci. 66(20): 4757–4770.
[3] X. Hua, J. Curtis, Y. Guo, B. Hancock, W. Ketterhagen, C. Wassgren (2015), The internal loads, moments, and stresses in rod-like particles in a low speed, vertical axis mixer, Chem. Eng. Sci. 134: 581–598.
[4] K. J. Hanley, E. P. Byrne, K. Cronin, J. C. Oliveira, J. A. O'Mahony, M. A. Fenelon (2011), Effect of pneumatic conveying parameters on physical quality characteristics of infant formula, J. Food Eng. 106(3): 566 236–244.
[5] J. Reppenhagen, J. Werther (2000), Catalyst attrition in cyclones, Powder Technol. 113(1-2): 55–69.
[6] G. Lu, J. R. Third, C. R. Müller (2015), Discrete element models for non-spherical particle systems: From theoretical developments to applications, Chem. Eng. Sci. 127: 425–465.
[7] P. W. Cleary, R. D. Morrison (2016), Comminution mechanisms, particle shape evolution and collision energy partitioning in tumbling mills, Minerals Eng. 86: 75–95.
[8] E. J. Garboczi (2002), Three-dimensional mathematical analysis of particle shape using X-ray tomography and spherical harmonics: Application to aggregates used in concrete, Cem. Concr. Res. 32(10): 1621–1638.
[9] J. F. Bloore (1977), The shape of pebbles, Math. Geol. 9: 113–122.
[10] I. Deiros Quintanilla, G. Combe, F. Emeriault, C. Voivret, J. Ferellec (2019), X-ray CT analysis of the evolution of ballast grain morphology along a Micro-Deval test: key role of the asperity scale, Granul. Matter 21: 30-1–30-12.